媒介変数(二次元)で表された曲線の長さL
導入
媒介変数表示の定義
yがxの関数であり、
xとyがそれぞれt(tは変数)の関数であるとき、
x = g(t), y = h(t)をまとめてtの媒介変数表示といい、
tを媒介変数という。
例えば、y = 4x^2は、tを用いて
逆に媒介変数表示からもとの関数を求めたい時は、
連立方程式を解くようにtを消去すれば良い。
例えば、x = 2t+1 , y = 3tを求めると、
x = 2t+1の両辺にそれぞれ-1を足したあと、2で割ると、
またxの定義域はtは実数全体(定義域が明示されていない場合はほぼ実数)であるから、
x = 2t+1より実数全体。
定義
x = g(t), y = h(t)の媒介変数表示を考える。
陽関数と同様に、t=0からt=bまでの曲線の長さLは、
ここで重要なのは、媒介変数表示では点の軌跡が重複する場合があるということ。
例えば、
証明
教科書に書いてある方法と上記の陽関数で利用した方法の2つを示す。
(上記の陽関数で利用した方法)
(教科書の方法)
微小部分を考えることによって求積する。
例えば、微小な面積を考えて面積を求積するなど。
教科書に書いてあるやり方はだいたいこれ。
面積でも、曲線の長さでも、体積でも微小部分を考えることによって求積している。
x = g(t), y = h(t)で表された曲線をCとする。
ここで、t=aからt=zまでのCの長さをL(z)とする。
今、上記の陽関数の曲線の長さを一つの直線で近似する方法を思い出してほしい。
媒介変数表示でも同様に一つの直線で近似でき、
応用
座標平面上で動く点の一瞬の速さ
一瞬の速さを求める前に、その概念の元となる一瞬の変化率について説明します。
導関数の定義とほぼ同じですが、
関数f(x)におけるx=aの一瞬の変化率とは、
なので、(1)と(2)が等しくない時一瞬の変化率は存在しない。
例えば、y = |x|はx = 0の一瞬の変化率は存在しない。||は絶対値を表す。
y = |x|のグラフ
一瞬の変化率なんてものは、結局割合を一般化したものに過ぎないということです。
本題
で進む時、]
a秒からb秒までに進んだ距離Lは、
極方程式で表された曲線の長さ
これは瞬殺である。
導入
極座標の定義
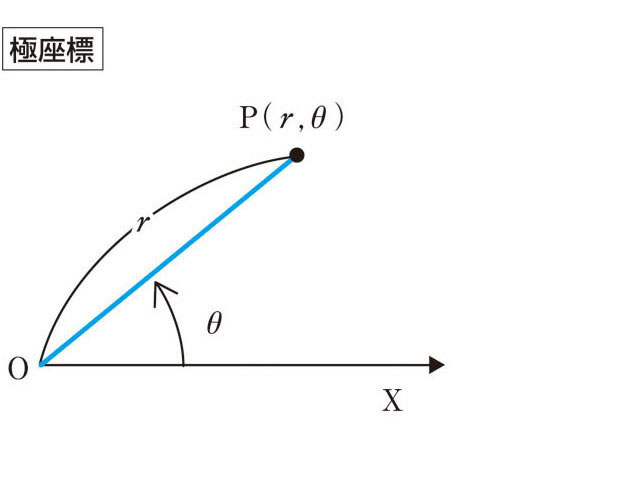
図を用いて説明する。
図のOは座標平面上の原点を表し、
直線OXはX軸を表す。
また極座標では原点Oを極といい、X>0とするときOXを始線という。
ここで半直線OX上(X>0とする)に点P'を取り、
線分OP'を反時計回りにθラジアン回転した線分を線分OPとする。
このとき、θラジアンを点Pの偏角といい、線分OPの長さrを点Pの大きさという。
すなわち、点Pを極座標で表すと点(r, θ)となる。
点(r, θ)のように書く。※点(r, θラジアン)とかいてもいい。
イメージは下記の図を参考にすると良い。
極方程式の定義
例えば、中心点が原点で半径がaの円周上の点pを極座標で表すと、
p(a, θ)である。
このとき、点pの極方程式はr = a という。
a = 2のときの円を極座標上で描いたもの。極方程式はr=2である。
すなわち、点pの極座標が(f(θ), θ)(θはある範囲)で表される時、
点pの極方程式はr = f(θ) (θはある範囲)という。
極方程式で表されるいろいろな図形
極方程式の媒介変数表示
点Pの極座標(r,θ)の媒介変数表示は、
証明